Answer:
Both plans would charge the same amount when 900 minutes per month are used.
Explanation:
Plan A: 700 free minutes + 15 cents per minute over 700 ($40)
Plan B: 500 free minutes + 5 cents per minute over 500 ($50)
1 cent = 0.01$
15 cent = 0.15$
5 cents = 0.05$
The charges for x minutes (assumed x>700) for plan A will be
40+0.15(x-700)
The charges for x minutes (assumed x>500) for plan B will be
50+0.05(x-500)
To find the value of x where both charges are the same, we equate
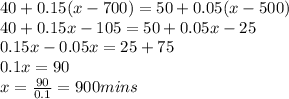
Hence,both plans would charge the same amount when 900 minutes per month are used.