Question

A 25 kg child at a playground runs with an initial speed of 2.5 m/s along a path tanget to the rim of a merry-go-round with a radius of 2.0 m and jumps on. The merry-go-round, which is initially at rest, has a moment of inertia of 500 kg m2. Find the angular velocity of the child and merry-go-round. Hint: the child and the merry-go-round form a system.

Answer 1

the angular velocity of the child and merry-go-round= 0.21 rad/sec

Step-by-step explanation:

mass m= 25 kg

initial speed v_i= 2.5 m/s

radius of merry go round= 2.0 m

MOI = 500 Kg-m^2

The angular momentum of the child is given by

L=mvr

initial angular momentum

Li=25×2.5×2= 125 kg m^2 s^{-1}

The final angular momentum considering the child and the merry-go-round form a system

`L_f= (I_D+ I_C)\omega`

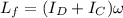
MOI of child I_C= 25×2^2= 25×4= 100 Kg-m^2

now plugging values in the above equation

`L_f= (500+ 100)\omega`

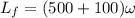
L_f= 600ω

Now , we know that the angular momentum is conserved we can write

Li =Lf

125= 600ω

⇒ω=125/600 = 0.21 rad/sec

the angular velocity of the child and merry-go-round= 0.21 rad/sec