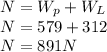Question

A 15 m ladder whose weight is 312 N is placed against a smooth vertical wall. A person whose weight is 579 N stands on the ladder a distance 2.4 m up the ladder. The foot of the ladder rests on the floor 6.45 m from the wall.

a) Calculate the force exerted by the wall. Answer in units of N.
b) Calculate the normal force exerted by the floor on the ladder. Answer in units of N.

Answer 1

a)

118.6 N

b)

891 N

Step-by-step explanation:

a)

In triangle ADE

`Cos\theta = (AE)/(AD)  = (6.45)/(15) \\Cos\theta = 0.43\\\theta = Cos^(-1)(0.43)\\\theta = 64.5`

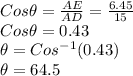
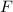`F` = Force applied by the wall on the ladder

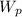`W_(p)` = weight of the person = 579 N

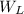`W_(L)` = weight of the ladder = 312 N

Using equilibrium of torque about point A

`F Sin\theta (AD) = W_(L) Cos\theta (AC) + W_(p) Cos\theta (AB)\\F Sin64.5 (15) = (312) Cos64.5 (7.5) + (579) Cos64.5 (2.4)\\F = 118.6 N`

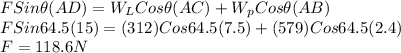
b)

Using equilibrium of force in vertical direction

`N = W_(p) + W_(L)\\N = 579 + 312\\N = 891 N`