Answer:
a)
118.6 N
b)
891 N
Step-by-step explanation:
a)
In triangle ADE
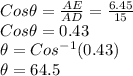
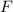 = Force applied by the wall on the ladder
= Force applied by the wall on the ladder
 = weight of the person = 579 N
= weight of the person = 579 N
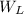 = weight of the ladder = 312 N
= weight of the ladder = 312 N
Using equilibrium of torque about point A
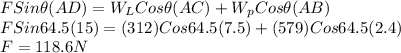
b)
Using equilibrium of force in vertical direction
