Question

After drawing the line y = 2x − 1 and marking the point A = (−2, 7), Kendall is trying to decide which point on the line is closest to A. The point P = (3, 5) looks promising. To check that P really is the point on y = 2x − 1 that is closest to A, what should Kendall do? Is P closest to A?

Answer 1

Explanation:

Having drawn the line, Kendall must verify that the point P belongs to the line y = 2x-1 and then calculate the distance between A-P and verify if it is the closest to A or there is another one of the line

Having the point P(3,5) substitue x to verify y

y=2*(3)-1=6-1=5 (3,5)

Now if the angle formed by A and P is 90º it means that it is the closest point, otherwise that point must be found

`d_(AP)=\sqrt{(y_(2)-y_(1))^(2)+(x_(2)-x_(1))^(2)}=\sqrt{(5-7)^(2)+(3-(-2}))^(2)}=\\\sqrt{(-2)^(2)+(5)^(2)}=√(29)`

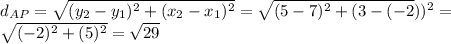
and we found the distance PQ and QA

;
`d_(PQ)=√(125)`,
`d_(QA)=12`

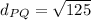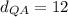
be the APQ triangle we must find <APQ through the cosine law (graph 2).