Answer:
Option d
Explanation:
given that a, b, c, and d be non-zero real numbers.
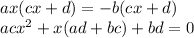
we can factorise this equation by grouping
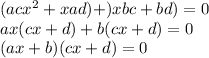
Equate each factor to 0 to get
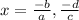
Ratio of one solution to another would be

So ratio would be ad/bc
Out of the four options given, option d is equal to this
So option d is right