Question

A special electronic sensor is embedded in the seat of a car thattakes riders around a circular loop-the-loop at an amusement park.The sensor measures the magnitude of the normal force that the seatexerts on a rider. The loop-the-loop ride is in the vertical planeand its radius is 24 m. Sitting on the seat before the ride starts,a rider is level and stationary, and the electronic sensor reads990 N. At the top of the loop, the rider is upside-down and moving,and the sensor reads 360 N. What is the speed of the rider at thetop of the loop?

Answer 1

17.91803 m/s

Step-by-step explanation:

r = Radius of loop = 24 m

W = Weight = 990 N

N = Apparent weight at top of loop = 360 N

g = Acceleration due to gravity = 9.81 m/s²

Mass of person

`m=(W)/(g)\\\Rightarrow m=(990)/(9.81)\\\Rightarrow m=100.917\ kg`

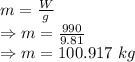
As all the forces are conserved at the top of the loop

`N+mg=ma\\\Rightarrow N+mg=m(v^2)/(r)\\\Rightarrow v=\sqrt{((N+mg)r)/(m)}\\\Rightarrow v=\sqrt{((360+990)* 24)/(100.917)}\\\Rightarrow v=17.91803\ m/s`

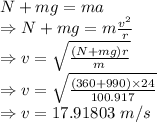
The speed of the rider at the top of the loop is 17.91803 m/s

Answer 2

v = 17.9 m/s

Step-by-step explanation:

As we know that the normal force measured by the sensor before the ride is started is given as

`F_n = mg = 990 N`

now when the rider has reached at the top position of the loop then the normal force is given as

`F_n' = 360 N`

now at the top position we have

`F_n' + mg = ma`

`F_n' + mg = (mv^2)/(R)`

so we have

`990 + 360 = (990 v^2)/(9.8 * 24)`

`v = 17.9 m/s`