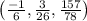Question

What is the solution of the system of equations negative 3x - 4y - 3z equals -7 2 x - 6 y + 2 Z equals 3 5 x - 2 y + 5 Z equals 9

Answer 1

The solution of the system of equations negative 3x - 4y - 3z equals -7 2 x - 6 y + 2 Z equals 3 5 x - 2 y + 5 Z equals 9(x, y, z) is
`\left((-1)/(6), (3)/(26), (157)/(78)\right)`

Solution:

Given, system of equations are

3x – 4y – 3z = - 7 ----- eqn (1)

2x – 6y + 2z = 3 ------ eqn (2)

5x – 2y + 5z = 9 ---- eqn (3)

We have to find the solution of the equations.

Now, from eqn (2)

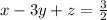`x-3 y+z=(3)/(2)` ----- eqn 4

Multiply eqn 4 with 5

`5 x-15 y+5 z=(15)/(2)`

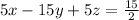
Now subtract eqn 5 from eqn 3

5x – 2y + 5z = 9

5x – 15y + 5z = 15/2

(-)-----------------------------------

0 + 13y + 0 = 9 - 15/2

`\begin{array}{l}{13 y=(18-15)/(2)} \\\\ {y=(3)/(26)}\end{array}`

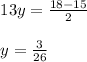
Now, perform eqn (1) + 3 x eqn (1)

3x – 4y – 3z = - 7

3x – 9y + 3z = 9/2

(+) -------------------------------------

6x – 13y = - 7 + 9/2

`\begin{array}{l}{6 x-13 * (3)/(26)=(9-14)/(2)} \\\\ {6 x-(3)/(2)=(-5)/(2)} \\\\ {6 x=-1} \\\\ {x=(-1)/(6)}\end{array}`

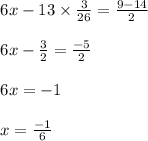
Then from eqn (4)

`\begin{array}{l}{(-1)/(6)-3 * (3)/(26)+z=(3)/(2)} \\\\ {z=(3)/(2)+(9)/(26)+(1)/(6)} \\\\ {z=(39+9)/(26)+(1)/(6)} \\\\ {z=(48)/(26)+(1)/(6)} \\\\ {z=(24)/(13)+(1)/(6)=(157)/(78)}\end{array}`

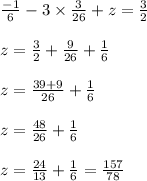
Hence, the solution is (x, y, z) is
`\left((-1)/(6), (3)/(26), (157)/(78)\right)`