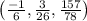The solution of the system of equations negative 3x - 4y - 3z equals -7 2 x - 6 y + 2 Z equals 3 5 x - 2 y + 5 Z equals 9(x, y, z) is
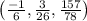
Solution:
Given, system of equations are
3x – 4y – 3z = - 7 ----- eqn (1)
2x – 6y + 2z = 3 ------ eqn (2)
5x – 2y + 5z = 9 ---- eqn (3)
We have to find the solution of the equations.
Now, from eqn (2)
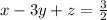 ----- eqn 4
----- eqn 4
Multiply eqn 4 with 5
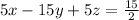
Now subtract eqn 5 from eqn 3
5x – 2y + 5z = 9
5x – 15y + 5z = 15/2
(-)-----------------------------------
0 + 13y + 0 = 9 - 15/2
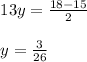
Now, perform eqn (1) + 3 x eqn (1)
3x – 4y – 3z = - 7
3x – 9y + 3z = 9/2
(+) -------------------------------------
6x – 13y = - 7 + 9/2
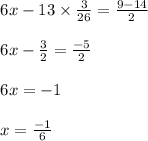
Then from eqn (4)
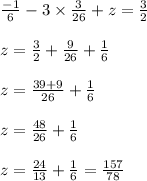
Hence, the solution is (x, y, z) is