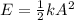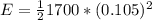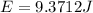To solve this problem it is necessary to apply the concepts related to the frequency in a spring, the conservation of energy and the total mechanical energy in the body (kinetic or potential as the case may be)
PART A) By definition the frequency in a spring is given by the equation
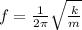
Where,
m = mass
k = spring constant
Our values are,
k=1700N/m
m=5.3 kg
Replacing,

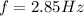
PART B) To solve this section it is necessary to apply the concepts related to the conservation of energy both potential (simple harmonic) and kinetic in the spring.
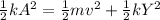
Where,
k = Spring constant
m = mass
y = Vertical compression
v = Velocity
This expression is equivalent to,
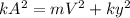
Our values are given as,
k=1700 N/m
V=1.70 m/s
y=0.045m
m=5.3 kg
Replacing we have,
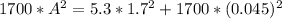
Solving for A,



PART C) Finally, the total mechanical energy is given by the equation