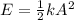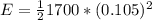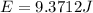Question

A 5.30kg block hangs from a spring with a spring constant 1700 N/m. The block is pulled down 4.50cm from the equilibrium position and given an initial velocity of 1.70 m/s back toward equilibrium. a) what is the frequency of the motion (units: Hz) b) what is the amplitude (units: m) c) what is the total mechanical energy of the motion (units: J)

Answer 1

To solve this problem it is necessary to apply the concepts related to the frequency in a spring, the conservation of energy and the total mechanical energy in the body (kinetic or potential as the case may be)

PART A) By definition the frequency in a spring is given by the equation

`f = (1)/(2\pi) \sqrt{(k)/(m)}`

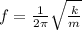
Where,

m = mass

k = spring constant

Our values are,

k=1700N/m

m=5.3 kg

Replacing,

`f = (1)/(2\pi) \sqrt{(1700)/(5.3)}`

`f=2.85 Hz`

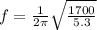
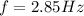
PART B) To solve this section it is necessary to apply the concepts related to the conservation of energy both potential (simple harmonic) and kinetic in the spring.

`(1)/(2)kA^2 = (1)/(2)mv^2 + (1)/(2) kY^2`

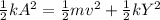
Where,

k = Spring constant

m = mass

y = Vertical compression

v = Velocity

This expression is equivalent to,

`kA^2 =mV^2 +ky^2`

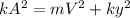
Our values are given as,

k=1700 N/m

V=1.70 m/s

y=0.045m

m=5.3 kg

Replacing we have,

`1700*A^2=5.3*1.7^2 +1700*(0.045)^2`

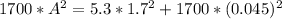
Solving for A,

`A^2 = (5.3*1.7^2 +1700*(0.045)^2)/(1700)`

`A ^2 = 0.011035`

`A=0.105 m \approx 10.5 cm`

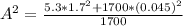
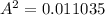
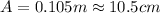
PART C) Finally, the total mechanical energy is given by the equation

`E = (1)/(2)kA^2`

`E=(1)/(2)1700*(0.105)^2`

`E= 9.3712 J`