Question

The altitude (i.e., height) of a triangle is increasing at a rate of 2.5 cm/minute while the area of the triangle is increasing at a rate of 2.5 square cm/minute. At what rate is the base of the triangle changing when the altitude is 7 centimeters and the area is 84 square centimeters?

Answer 1

The base is decreasing at a rate of 7.8571 centimeters per minute.

Explanation:

We are given the following information in the question:

The height of a triangle is increasing at a rate of 2.5 cm/minute

`\displaystyle(dh)/(dt) = 2.5 \text{ cm per minute}`

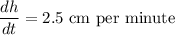
The area of the triangle is increasing at a rate of 2.5 square cm/minute.

`\displaystyle(dA)/(dt) = 2.5 \text{ square cm per minute}`

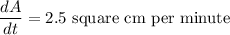
Area of triangle is given by:

`A = \displaystyle(1)/(2)* b* h`

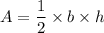
where A is the area of triangle, b is the base of triangle and h is the height of the triangle.

Differentiating, we get,

`A = \displaystyle(1)/(2)* b* h\\\\(dA)/(dt) = (1)/(2)\Bigg(b(dh)/(dt) + h(db)/(dt)\Bigg)`

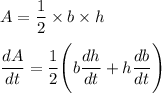
We have to find rate of change of base of the triangle when the altitude is 7 centimeters and the area is 84 square centimeters

h = 7 cm

A = 84 square centimeters

`84 = \displaystyle(1)/(2)* 7* b\\\\b = 24\text{ cm}`

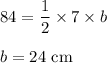
Putting the values, we get:

`\displaystyle(dA)/(dt) = (1)/(2)\Bigg(b(dh)/(dt) + h(db)/(dt)\Bigg)\\\\2.5 = (1)/(2)\Bigg((24)(2.5) + (7)(db)/(dt)\Bigg)\\\\5 - 60 = 7(db)/(dt)\\\\(dh)/(dt) =-7.8571\text{ cm per minute}`

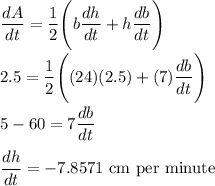
Thus, the base is decreasing at a rate of 7.8571 centimeters per minute.