There are 2118760 ways to select a committee of 5 senators be formed if no state may be represented more than once
Solution:
Given that, There are 100 members of the U.S. Senate with 2 members from each state.
Which means there are senates from 100/2 = 50 states.
We have to find in how many ways can a committee of 5 senators be formed if no state may be represented more than once?
As no state can be represented more than once, we just have to take 1 from each state for selections.
So, now we will have 50 senators out of who we have to pick 5 senators.
As we just have to select the senators. We can use combinations here.
In combinations, to pick r items from n items, there will be
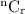 ways
ways
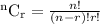
Then, here we have to pick 5 out of 50:
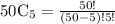

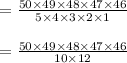
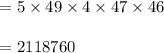
Hence, there are 2118760 ways to select.