Answer:
It depends on the relation between the heights of both pyramids
Explanation:
We know the volume of a pyramid of base b and height h is
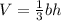
If the volume of the pyramid A is 3 times the volume of the pyramid B, then
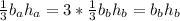
Which means

If we knew both heights are the same, we could conclude that
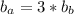
In which case the base of the pyramid A would be greater than the other base
But if, for example, the height of the pyramid A is 3 times the height of the other height, then
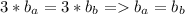
Both bases would be the same.
If we choose that
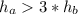
it would mean
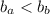
In which case the base of the pyramid A would be less than the other base
So the answer entirely depends on the relation between the heights of both pyramids