Answer:
a)
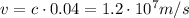
b)
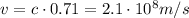
c)
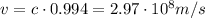
d)
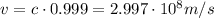
e)
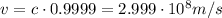
Step-by-step explanation:
At that energies, the speed of proton is in the relativistic theory field, so we need to use the relativistic kinetic energy equation.
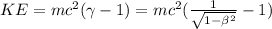 (1)
(1)
Here β = v/c, when v is the speed of the particle and c is the speed of light in vacuum.
Let's solve (1) for β.
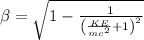
We can write the mass of a proton in MeV/c².
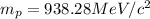
Now we can calculate the speed in each stage.
a) Cockcroft-Walton (750 keV)
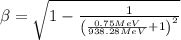
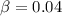
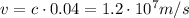
b) Linac (400 MeV)
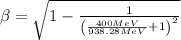
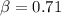
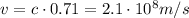
c) Booster (8 GeV)
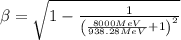
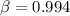
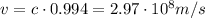
d) Main ring or injector (150 Gev)
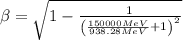
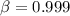
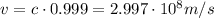
e) Tevatron (1 TeV)
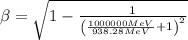
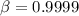
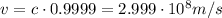
Have a nice day!