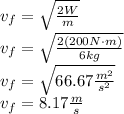Question

A force in the +x-direction with magnitude ????(x) = 18.0 N − (0.530 N/m)x is applied to a 6.00 kg box that is sitting on the horizontal, frictionless surface of a frozen lake. ????(x) is the only horizontal force on the box. If the box is initially at rest at x = 0, what is its speed after it has traveled 14.0 m?

Answer 1

`v_f=8.17(m)/(s)`

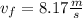
Step-by-step explanation:

First, we calculate the work done by this force after the box traveled 14 m, which is given by:

`W=\int\limits^(x_f)_(x_0) {F(x)} \, dx \\W=\int\limits^(14)_(0) ({18N-0.530(N)/(m)x}) \, dx\\W=[(18N)x-(0.530(N)/(m))(x^2)/(2)]^(14)_(0)\\W=(18N)14m-(0.530(N)/(m))((14m)^2)/(2)-(18N)0+(0.530(N)/(m))(0^2)/(2)\\W=252N\cdot m-52N\cdot m\\W=200N\cdot m`

Since we have a frictionless surface, according to the the work–energy principle, the work done by all forces acting on a particle equals the change in the kinetic energy of the particle, that is:

`W=\Delta K\\W=K_f-K_i\\W=(mv_f^2)/(2)-(mv_i^2)/(2)`

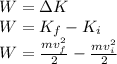
The box is initially at rest, so
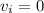`v_i=0`. Solving for
`v_f`:

`v_f=\sqrt{(2W)/(m)}\\v_f=\sqrt{(2(200N\cdot m))/(6kg)}\\v_f=\sqrt{66.67(m^2)/(s^2)}\\v_f=8.17(m)/(s)`