Answer:
v = 13.75 m/s
Step-by-step explanation:
mass of rod (m) = 0.147 kg
spring constant (k) = 32800 N/m
initial compression (Y1) = 4.44 cm = 0.0444 m
final compression (Y2) = 1.53 cm = 0.0153 m
find the speed at the instant of contact
kinetic energy of a spring = elastic potential energy
0.5m
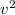 = 0.5k
= 0.5k

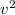 =
=
![\frac{0.5k[tex]x^(2)]() }{0.5m} \[/tex]
}{0.5m} \[/tex]
where x = Y1 - Y2
x = 0.0444 - 0.0153 = 0.0291 m
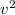 =
=
![\frac{0.5 x 32800 x [tex]0.0291^(2)]() }{0.5 x 0.147} \[/tex]
}{0.5 x 0.147} \[/tex]
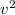 = 188.95
= 188.95
v = 13.75 m/s