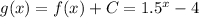Question

What is the equation of the function shown in the graph, given the equation of the parent function is f(x)=1.5x ?

g(x)=1.5x−2

g(x)=1.5x−3

g(x)=1.5x−4

g(x)=1.5x+2
An exponential function on a coordinate plane with x and y axis in increments of 1 increasing from negative 5 to 5. The function increases from left to right beginning infinitely close in the third quadrant to a dashed horizontal line at y equals negative 4. The function increases through begin ordered pair 0 comma negative 3 end ordered pair and continues to increase through begin ordered pair 2 comma negative 1.75 end ordered pair. The function continues to increase through the second quadrant and out of the first quadrant.

Answer 1

D

Explanation:

Answer 2

`g(x)=1.5^(x)-4`

Explanation:

Given:

The parent function is given as:

`f(x)=1.5^(x)`

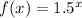
Let us consider a point on
`f(x)\ and\ g(x)` and compare their transformation.

The easiest point to consider is the y-intercept. At the y-intercept, the value of 'x' is 0.

The y-intercept of the function
`f(x)` is for
`x=0`. So,

`f(0)=1.5^(0)=1`

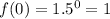
The y-intercept of
`f(x)` is the point (0, 1).

Now, as per question, the transformed function
`g(x)` passes through the point (0, -3). Therefore,

The function
`g(x)` in the graph has the y-intercept equal to -3 as at y-intercept, the 'x' value is 0.

Therefore, the y-intercept of
`g(x)` is the point (0,-3).

Now, consider the transformation for the points (0, 1) and (0, -3).

`(0,1)\rightarrow (0,-3)`

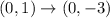
Here, the 'x' value remains the same but the 'y' values decreases by 4 units. So, the rule will be:

`(x,y)\rightarrow (x,y-4)`

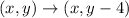
As per translation rules, if C units is added to 'y' value, then the graph moves up if 'C' is positive and moves down if 'C' is negative.

Also, the equation is of the form:
`g(x)=f(x)+C`

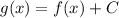
Here,
`C=-4`.

Therefore, the graph shifts down by 4 units.

The equation of the function
`g(x)` is given as:

`g(x)=f(x)+C=1.5^(x)-4`