Question

A 35-ft long solid steel rod is subjected to a load of 8,000 lb. This load causes the rod to stretch 0.266 in. The modulus of elasticity of the steel is 30,000,000 psi. Determine the diameter of the rod (precision of 0.00).

Answer 1

Diameter of rod = 19 mm

Explanation:

We have the equation for elongation

`\Delta L=(PL)/(AE)\\\\A=(\pi d^2)/(4)`

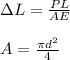
Here we have

Elongation, ΔL = 0.266 in = 0.00676 m

Length , L = 35 ft = 10.668 m

Load, P = 8000 lb = 35585.77 N

Modulus of elasticity, E = 30,000,000 psi = 2.07 x 10¹¹ N/m²

Substituting

`\Delta L=(PL)/(AE)\\\\A=(\pi d^2)/(4)\\\\\Delta L=(4PL)/(\pi d^2E)\\\\d^2=(4PL)/(\pi \Delta LE)\\\\d=\sqrt{(4PL)/(\pi \Delta LE)}\\\\d=\sqrt{(4* 35585.77* 10.668)/(\pi * 0.00676 * 2.07* 10^(11))}=0.019m\\\\d=19mm`

Diameter of rod = 19 mm