To solve this problem it is necessary to apply the concepts related to relativity.
The distance traveled by the light and analyzed from an observer relative to it is established as
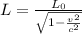
Where,
L = Length
c = Speed of light (7.58m/s at this case)
v = Velocity
Our velocity can be reached by kinematic motion equation, where
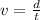
Here,
d = Distance
t = Time
Replacing


Replacing at the previous equation,
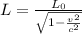
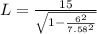
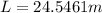
Therefore the distance covered, according to the catcher who is standing at home plate is 24.5461m