Question

Assume that the speed of light in a vacuum has the hypothetical value of 7.58 m/s. In a pickup baseball game, a runner runs at a constant velocity from third base to home plate in a time of 2.50 s, according to the runner. Also according to the runner, the distance covered is 15.0 m. What is the distance covered, according to the catcher who is standing at home plate?

Answer 1

To solve this problem it is necessary to apply the concepts related to relativity.

The distance traveled by the light and analyzed from an observer relative to it is established as

`L = \frac{L_0}{\sqrt{1-(v^2)/(c^2)}}`

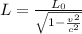
Where,

L = Length

c = Speed of light (7.58m/s at this case)

v = Velocity

Our velocity can be reached by kinematic motion equation, where

`v = (d)/(t)`

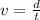
Here,

d = Distance

t = Time

Replacing

`v = (15)/(2.5)`

`v = 6m/s`

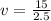
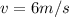
Replacing at the previous equation,

`L = \frac{L_0}{\sqrt{1-(v^2)/(c^2)}}`

`L = \frac{15}{\sqrt{1-(6^2)/(7.58^2)}}`

`L = 24.5461m`

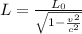
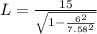
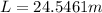
Therefore the distance covered, according to the catcher who is standing at home plate is 24.5461m