Answer:
a) 8, multiplicity 2; 8, multiplicity 3
Step-by-step explanation:
Remember that a is a zero of the polynomial f(x) if f(a)=0 and has multiplicity n if the termn (x-a) is n times in the factorization of f(x).
We have that
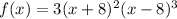
Observe that
1.

and (x+8) appear two times in the factorization of f(x). Then -8 is a zero of f(x) with multiplicity 2.
2.
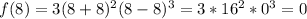
and and (x - 8) appear three times in the factorization of f(x). Then 8 is a zero of f(x) with multiplicity 3.
Since f(x) has degree 5 and the sum of the multiplicities is 5 then f(x) hasn't more zeros.