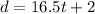Answer:
The linear model of Greg's car is given by:

The linear model of Marti's car is given by:
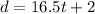
Explanation:
Let:
 represent distance traveled by the cars in feet.
represent distance traveled by the cars in feet.
 represent time of travel in seconds.
represent time of travel in seconds.
Greg's Car:
Given:
Rate of change = 13 ft/s
After 2 seconds his car was 30.7 feet.
From the given data we have the following:
Slope of line
 = 13 ft/s
= 13 ft/s
Point
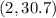
Using point slope equation to model the linear relationship.

where
 is a point on line.
is a point on line.
So, we have:
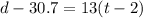
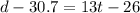 [ Using distribution.]
[ Using distribution.]
Adding 30.7 to both sides.
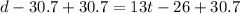

The linear model of Greg's car is given by:

Marti's car:
Given:
Rate of change = 16.5 ft/s
Starting point = 2 ft
From the given data we have the following:
Slope of line
 = 16.5 ft/s
= 16.5 ft/s
y-intercept = 2 ft
Using slope intercept equation to model the linear relationship.

where
 is slope of line or rate of change and
is slope of line or rate of change and
 is the y-intercept or stating point.
is the y-intercept or stating point.
So, we have:
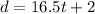
The linear model of Marti's car is given by: