Question

Certain neutron stars (extremely dense stars) are believed to be rotating at about 1 rev/s. If such a star has a radius of 20 km, what must be its minimum mass so that material on its surface remains in place during the revis's rotation?

Answer 1

Mass,
`M=4.73* 10^(24)\ kg`

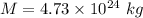
Step-by-step explanation:

It is given that,

Angular velocity of the neutron stars,
`\omega=1\ rev/s=6.28\ rad/s`

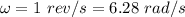
Radius of the star, r = 20 km = 20000 m

Let M is the mass of the star. The magnitude of acceleration due to gravity is balanced by the centripetal acceleration of the stars.

`(GM)/(r^2)=\omega^2r`

`M=(\omega^2r^3)/(G)`

`M=((6.28)^2* (20000)^3)/(6.67* 10^(-11))`

`M=4.73* 10^(24)\ kg`

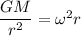
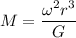
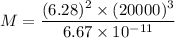
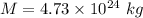
So, the minimum mass so that material on its surface remains in place during the revis's rotation is
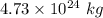`4.73* 10^(24)\ kg`. Hence, this is the required solution.