Answer:
Time period, T = 403.78 years
Step-by-step explanation:
It is given that,
Orbital distance,
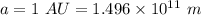
Mass of the Earth,
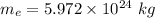
Mass of the planet,

Let T is the orbital period of this planet. The Kepler's third law of motion gives the relation between the orbital period and the orbital distance.
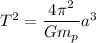

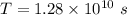
or
T = 403.78 years
So, the orbital period of this planet is 404 years. Hence, this is the required solution.