Question

Consider the sequence: 8, 11, 14, 17, 20, 23, 26, ..... Write a recursive definition: Group of answer choices

LaTeX: a_n=2\cdot a_{n-1}-5 a n = 2 ⋅ a n − 1 − 5
LaTeX: a_n=3\cdot a_{n-1} a n = 3 ⋅ a n − 1
LaTeX: a_n=3+a_{n-1} a n = 3 + a n − 1
LaTeX: a_n=8+3\cdot a_{n-1}

Answer 1

Consider the sequence: 8, 11, 14, 17, 20, 23, 26, The recursive definition is
`a_(n)=3+a_(n-1)`

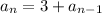
Solution:

The given sequence is :- 8, 11, 14, 17, 20, 23, 26, .....

`\text { The first term is } a_(1)=8`

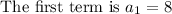
Second term is
`a_2 = 11` and so on

On analyzing the above series we can say

Each time we want a new term, we add on 3 to previous term which is as follows:-

8 + 3 = 11

11 + 3 = 14

14 + 3 = 17

17 + 3 = 20

20 + 3 = 23

23 + 3 = 26

And so on

This recursive step of adding on 3 to the prior term is written in the following general form:

`a_(n)=3+a_(n-1)`

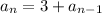
Let's check the above recursive definition by substituting n = 2 we should get 11

`a_2 = 3 + a_(2-1)\\\\a_2 = 3 + a_(1)\\\\a_2 = 3 + 8 = 11`

Thus the required recursive definition is found