Consider the sequence: 8, 11, 14, 17, 20, 23, 26, The recursive definition is
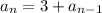
Solution:
The given sequence is :- 8, 11, 14, 17, 20, 23, 26, .....
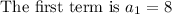
Second term is
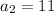 and so on
and so on
On analyzing the above series we can say
Each time we want a new term, we add on 3 to previous term which is as follows:-
8 + 3 = 11
11 + 3 = 14
14 + 3 = 17
17 + 3 = 20
20 + 3 = 23
23 + 3 = 26
And so on
This recursive step of adding on 3 to the prior term is written in the following general form:
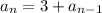
Let's check the above recursive definition by substituting n = 2 we should get 11
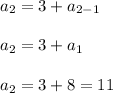
Thus the required recursive definition is found