Question

Determine whether the function is a linear transformation. T: P2 → P2, T(a0 + a1x + a2x2) = (a0 + a1 + a2) + (a1 + a2)x + a2x2.

Answer 1

Answer with Step-by-step explanation:

We are given that a function

`T:P_2\rightarrow P_2`

`T(a_0+a_1x+a_2x^2)=(a_0+a_1+a_2)+(a_1+a_2)x+a_2x^2`

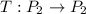
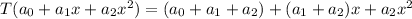
We have to determine the given function is a linear transformation.

If a function is linear transformation then it satisfied following properties

`1.T(x+y)=T(x)+T(y)`

2.
`T(ax)=aT(x)`

`T(a_0+a_1x+a_2x^2+b_0+b_1x+b_2x^2)=T((a_0+b_0)+(a_1+b_1)x+(a_2+b_2)x^2)=(a_0+b_0+a_1+b_1+a_2+b_2)+(a_1+b_1+a_2+b_2)x+(a_2+b_2)x^2`

`T(a_0+a_1x+a_2x^2+b_0+b-1x+b_2x^2)=(a_0+a_1+a_2)+(a_1+a_2)x+a_2x^2+(b_0+b_1+b_2)+(b_1+b_2)x+b_2x^2`

`T(a_0+a_1x+a_2x^2+b_0+b-1x+b_2x^2)=T(a_0+a_1x+a_2x^2)+T(b_0+b_1x+b_2x^2)`

`T(a(a_0+a_1x+a_2x^2))=T(aa_0+aa_1x+aa_2x^2)`

`T(a(a_0+a_1x+a_2x^2))=(aa_0+aa_1+aa_2)+(aa_1+aa_2)x+(aa_2)x^2`

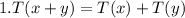
`T(a(a_0+a_1x+a_2x^2))=a(a_0+a_1+a_2)+a(a_1+a_2)x+aa_2x^2=a((a_0+a_1+a_2)+(a_1+a_2)x+a_2x^2)=aT(a_0+a_1x+a_2x^2)`

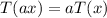
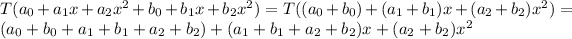
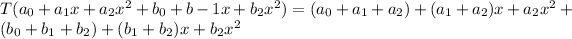
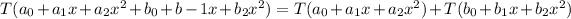
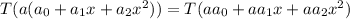
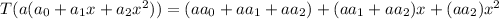
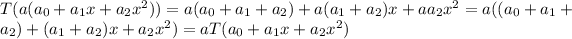
Hence, the function is a linear transformation because it satisfied both properties of linear transformation.