Question

A loop lies in a magnetic field, with the field perpendicular to the plane of the loop. Which does not induce a current in the loop?

a) Increasing the magnitude of the field
b) Rotating the loop around the diameter
c) Changing the direction of the field
d) Sliding the loop perpendicular to the field vector
e) Increasing the size of the loop

Answer 1

option (D)

Step-by-step explanation:

As the magnetic flux linked with the coil changes, the induced emf is developed in the coil. This is called one of the Farady's law of electromagnetic induction.

option (a) when the magnitude of magnetic field increases, the flux changes and hence an induced emf is developed.

option (B) As the loop rotates, the magnetic flux changes and hence the induced emf is developed.

option (C) As the direction of magnetic field changes, the magnetic flux changes and hence the induced emf is developed.

option (D) As the loop is sliding, so no magnetic flux changes and hence no induced emf is developed.

option (E) As the size of the loop increases, the magnetic flux changes and hence the induced emf is developed.

Answer 2

Option d

Step-by-step explanation:

From Maxwell's law, we know that;

`\Delta* \vec{E} = \frac{\delta {B}}{\delta t}`

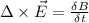
where

E = Electric Field

B = Magnetic Field

Also from Lenz Law:

emf, e = -
`(\delta \phi)/(\delta t)`

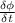
where

`\phi` = magnetic flux linkage

Now, in order for the current not to be induced in the loop, option a and c do not hold.

Since from the above equations, variation in both or any of the magnetic and electric fields will result in the induction of current as both are vector.

For the option b, if we rotate the loop about the diameter or increase the size or area of the loop, it will result in the change in its magnetic flux and current will be induced as is clear from the given equation:

`\phi = \vec{B}.\vec{A}`

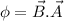
Now, in case of option d, if we consider a uniform magnetic field, then there won't be any variation and hence no current will be induced while we slide the wire perpendicular to the loop.