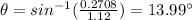Question

Sound with frequency 1270 Hz leaves a room through a doorway with a width of 1.12 m . At what minimum angle relative to the centerline perpendicular to the doorway will someone outside the room hear no sound? Use 344 m/s for the speed of sound in air and assume that the source and listener are both far enough from the doorway for Fraunhofer diffraction to apply. You can ignore effects of reflections.

Answer 1

The minimum angle is
`13.99^(\circ)`

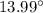
Solution:

As per the question:

Frequency of the sound, f = 1270 Hz

Width, d = 1.12

Velocity of sound, v = 344 m/s

Now,

We know that:

`v = f\lambda`

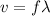
where

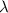`\lambda` = wavelength

Thus

`344 = 1270* \lambda`

`\lambda = 0.2708\ m`

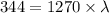
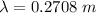
Now, for diffraction:

`n\lambda =dsin\theta`

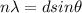
Now,

To calculate the minimum angle, we use the above eqn:

`\theta = sin^(- 1)((n\lambda)/(d))`

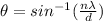
where

n = 1

`\theta = sin^(- 1)((0.2708)/(1.12)) = 13.99^(\circ)`