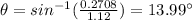Answer:
The minimum angle is
Solution:
As per the question:
Frequency of the sound, f = 1270 Hz
Width, d = 1.12
Velocity of sound, v = 344 m/s
Now,
We know that:
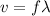
where
 = wavelength
= wavelength
Thus
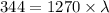
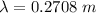
Now, for diffraction:
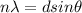
Now,
To calculate the minimum angle, we use the above eqn:
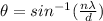
where
n = 1