Question

A single slit diffraction experiment performed with an argon laser of wavelength 454.6 nm produces a pattern on a screen with dark fringes (minima) separated by 10 mm. If we switch to a helium laser of wavelength 632.8 nm, without changing anything else in the setup, what will be the new separation between dark fringes? Select one:

a. 7.2 mm

b. 6.1 mm

c. 13.9 mm

d. 17.3 mm

e. 15.2 mm

Answer 1

To develop this problem it is necessary to apply the concepts related to Interference and the Two slit experiment.

Young's equation defines the separation between fringes this phenomenon as,

`d = (\lambda D)/(a)`

Where,

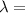`\lambda =` Wavelength

d = Separation between fringes

a = Slit width

D = Distance between the slits and screen

Then for the two case we have

`d_1 = (\lambda D)/(a_1)`

`d_2 = (\lambda D)/(a_2)`

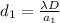
Calculating the new separation between the fringes would be

`(d_2)/(d_1) = ((\lambda D)/(a_1))/((\lambda D)/(a_2))`

`(d_2)/(d_1) = (\lambda_1)/(\lambda_2)`

`d_2= (\lambda_1)/(\lambda_2) d_1`

We have then,

`d_2 = (632.9*10^(-8))/(454.6*10^(-9)) 10*10^(-3)`

`d_2 = 13.9mm`

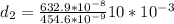
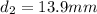
Therefore the correct answer is c.