To develop this problem it is necessary to apply the concepts related to Interference and the Two slit experiment.
Young's equation defines the separation between fringes this phenomenon as,
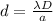
Where,
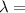 Wavelength
Wavelength
d = Separation between fringes
a = Slit width
D = Distance between the slits and screen
Then for the two case we have
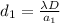
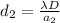
Calculating the new separation between the fringes would be
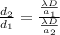

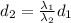
We have then,
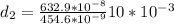
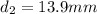
Therefore the correct answer is c.