Answer:
21
Explanation:
In order to form a chord you need to:
- Select one point. You have 7 choices
- Select a another point. You have just 6 choices because you have to dicard the point alredy chosen
- Connect the two points with a chorde
Since we have 7 choices for the first point and 6 for the second one, one might think that there are a total of 7*6 = 42 choices.
However the correct answer is 21, because you have to take into the account that selecting the point A first and selecting the point B on second step is the same than selecting the point B first and then the point A, because the chord is the same.
Therefore we are counting each chord twice, and we have to divide the result by 2, obtaining 7*6 / 2 = 21.
You can also calculate the amount by using the combiatorial number. The total amount of possibilities to select k elements from a set of n, with n higher than or equal to k and both positive, without taking into account the order is the combinatorial number of n with k, given by

In this case, in order to form a chord we need to select 2 points of the seven we are given, ignoring order, thus the total amount of possibilities is
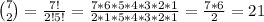
As we calculated before.