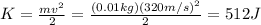Answer:
Step-by-step explanation:
Since the surface is frictionless, momentum will be conserved. If the bullet of mass
 has an initial velocity
has an initial velocity
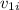 and a final velocity
and a final velocity
 and the block of mass
and the block of mass
 has an initial velocity
has an initial velocity
 and a final velocity
and a final velocity
 then the initial and final momentum of the system will be:
then the initial and final momentum of the system will be:
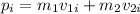
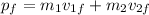
Since momentum is conserved,
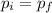 , which means:
, which means:
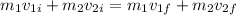
We know that the block is brought to rest by the collision, which means
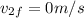 and leaves us with:
and leaves us with:
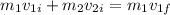
which is the same as:
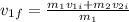
Considering the direction the bullet moves initially as the positive one, and writing in S.I., this gives us:

So kinetic energy of the bullet as it emerges from the block will be: