Answer: (1.1838, 1.1962)
Explanation:
The formula we use to calculate the confidence interval for population mean ( if population standard deviation is not given)is given by :-
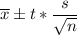 ,
,
where n= sample size
s= sample standard deviation.
 = sample mean
= sample mean
t* = Two-tailed critical t-value.
Given : n= 25
Degree of freedom : df = n-1 =24
Significance level
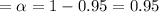
Now from students' t-distribution table , check the t-value for significance level
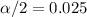 and df=24:
and df=24:
t*=2.0639
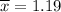 fluid ounces
fluid ounces
s= 0.015 fluid ounces
We assume that the population is approximately normally distributed
Now, the 95% two-sided confidence interval on the mean volume of syrup dispensed :-

∴ The required confidence interval = (1.1838, 1.1962)