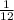The probability for choosing green and red is
Solution:
Given that , A bag contains 1 red, 1 yellow, 1 blue, and 1 green marble.
We have to find what is the probability of choosing a green marble, not replacing it, and then choosing a red marble?
Now, we know that,

So, total possible outcomes = 1 red + 1 yellow + 1 blue + 1 green = 4
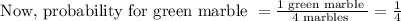
And now, total outcomes will be only 3 as we are not replacing the picked marble.
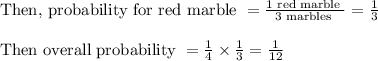
Hence, the probability for choosing green and red is