Question

What is the magnitude of the maximum stress that exists at the tip of an internal crack having a radius of curvature of 4.5 × 10-4 mm (1.772 × 10-5 in.) and a crack length of 3 × 10-2 mm (1.181 × 10-3 in.) when a tensile stress of 160 MPa (23210 psi) is applied?

Answer 1

To develop this problem it is necessary to apply the concepts related to stress.

The calculation of maximum stress by definition is given by

`\sigma_m = 2\sigma_0 \sqrt{((a)/(\rho_i))}`

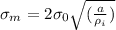
Where,

`\sigma_0` = Nominal applied tensile stress

a = Length of a surface crack

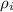`\rho_i` = Radius of curvature tip of the internal crack

Now we can find the length of a surface crack,

`a = (3*10^(-3))/(2)`

`a = 1.5*10^(-2)mm`

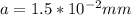
With this value we find now the ratio of
`\rho_t`

`(a)/(\rho_t) =(1.5*10^(-2)mm)/(4.5*10^(-4))`

`(a)/(\rho_t) = 33.33`

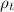
Therefore the magnitud of the stress would be

`\sigma_m = 2\sigma_0 \sqrt{((a)/(\rho_i))}`

`\sigma_m = 2(160Mpa) √((33.33))`

`\sigma_m = 1847.42 Mpa`

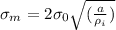
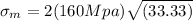
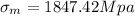
Therefore the magnitude of the maximum stress is 1847.42Mpa.