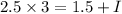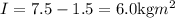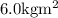 is the persons moment of inertia about an axis through her center of mass.
is the persons moment of inertia about an axis through her center of mass.
Answer: Option B
Step-by-step explanation:
Given data are as follows:
moment of inertia of the empty turntable = 1.5
Torque = 2.5 N/m , and
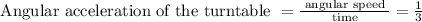
Let the persons moment of inertia about an axis through her center of mass= I
So, Now, from the formula of torque,
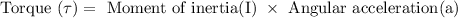
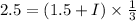
So, from the above equation, we can measure the person’s moment of Inertia (I)