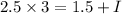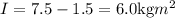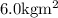Question

The moment of inertia of the empty turntable is 1.5 kg?m2. With a constant torque of 2.5 N?m, the turntableperson system takes 3.0 s to spin from rest to an angular speed of 1.0 rad/s. What is the persons moment of inertia about an axis through her center of mass? Ignore friction in the turntable axle.

The moment of inertia of the empty turntable is 1.5 . With a constant torque of 2.5 , the turntableperson system takes 3.0 to spin from rest to an angular speed of 1.0 . What is the persons moment of inertia about an axis through her center of mass? Ignore friction in the turntable axle.

2.5 kg?m2
6.0 kg?m2
7.5 kg?m2
9.0 kg?m2

Answer 1

`6.0 \mathrm{kg} \mathrm{m}^(2)` is the persons moment of inertia about an axis through her center of mass.

Answer: Option B

Step-by-step explanation:

Given data are as follows:

moment of inertia of the empty turntable = 1.5

Torque = 2.5 N/m , and

`\text { Angular acceleration of the turntable }=\frac{\text { angular speed }}{\text { time }}=(1)/(3)`

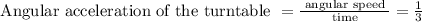
Let the persons moment of inertia about an axis through her center of mass= I

So, Now, from the formula of torque,

`\text { Torque }(\tau)=\text { Moment of inertia(I) } * \text { Angular acceleration(a) }`

`2.5=(1.5+I) * (1)/(3)`

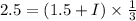
So, from the above equation, we can measure the person’s moment of Inertia (I)

`2.5 * 3=1.5+I`

`I=7.5-1.5=6.0 \mathrm{kg} m^(2)`