Answer:
Explanation:
- Let us assume, the contrary √3 is a rational no.
- √3 = p/q ,where p and q are co-prime
- p = √3q
- squaring on both sides
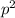 /3 =
/3 =
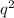 .............................(1)
.............................(1)- 3 is a factor of p
- p = 3c , where c is some constant
- substituting p = 3c in equation (1)
- 9
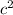 = 3
= 3
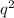
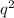 /3 =
/3 =
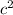
∴ 3 is also a factor of q
- But , this is a contradiction.
- we have assume p and q are co prime
∴ √3 is an irrational no.