To solve this problem it is necessary to apply the concepts related to the period based on variables such as gravity, distance and frequency.
By definition, know that the Period is
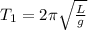
Where,
L = Length
g = Gravity
At the same time, frequency can be defined as,
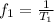
So using this for
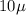 m we have that,
m we have that,
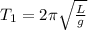
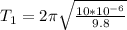
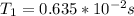
Then the frequency is
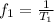
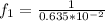
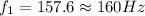
For the second length of 50\mu m we have that
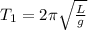
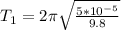
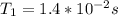
Then the frequency is
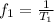
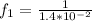
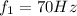
Therefore the correct answer is A.