Question

The length of stereocilia actually vary from 10 to 50 micrometers. Again, assuming that they behave like simple pendula, over what frequency range of sound waves would they resonate. (The actual frequency range of human hearing is 20 Hz 20,000 Hz, so might there be other mechanisms involved and/or might the pendular model be rather oversimplified?)

A. About 70 Hz -160 Hz.
B. About 440 Hz - 1000 Hz.
C. About 20 Hz - 50 Hz.
D. About 0.07 to 0.16 Hz.

Answer 1

To solve this problem it is necessary to apply the concepts related to the period based on variables such as gravity, distance and frequency.

By definition, know that the Period is

`T_1 = 2\pi \sqrt{(L)/(g)}`

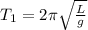
Where,

L = Length

g = Gravity

At the same time, frequency can be defined as,

`f_1 = (1)/(T_1)`

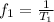
So using this for
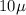`10\mu` m we have that,

`T_1 = 2\pi \sqrt{(L)/(g)}`

`T_1 = 2\pi \sqrt{(10*10^(-6))/(9.8)}`

`T_1 = 0.635*10^(-2)s`

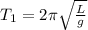
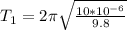
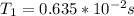
Then the frequency is

`f_1 = (1)/(T_1)`

`f_1 = (1)/(0.635*10^(-2))`

`f_1 = 157.6\approx 160Hz`

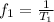
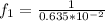
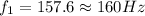
For the second length of 50\mu m we have that

`T_1 = 2\pi \sqrt{(L)/(g)}`

`T_1 = 2\pi \sqrt{(5*10^(-5))/(9.8)}`

`T_1 = 1.4*10^(-2)s`

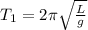
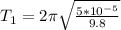
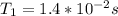
Then the frequency is

`f_1 = (1)/(T_1)`

`f_1 = (1)/(1.4*10^(-2))`

`f_1 = 70Hz`

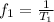
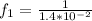
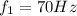
Therefore the correct answer is A.