Question

Plz prove this triangle congruence.

Answer 1

ΔDBE≅ΔQAP (by RHS criteria)

Explanation:

Given that,
`PQ=DE`,
`PB=AE`,
`QA`⊥
`PE`

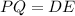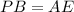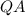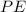
and
`DB`⊥
`PE`

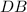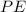
⇒∠PAQ=90° and ∠EBD=90°(definition of perpendicular lines)

Its given that PB=AE,

subtracting AB on both sides,

we get: PB-AE=AB-AE

⇒PA=EB (equals subtracted from equals, the remainders are equals)

Therefore, ΔDBE≅ΔQAP (by RHS criteria)

conditions for congruence:

• ∠DBE=∠QAP=90°(right angle)
• PQ=ED(hypotenuse)
• PA=EB(side)

So, ∡D=∡Q(as congruent parts of congruent triangles are equal)