Answer:
ΔDBE≅ΔQAP (by RHS criteria)
Explanation:
Given that,
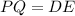 ,
,
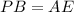 ,
,
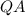 ⊥
⊥
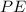
and
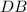 ⊥
⊥
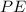
⇒∠PAQ=90° and ∠EBD=90°(definition of perpendicular lines)
Its given that PB=AE,
subtracting AB on both sides,
we get: PB-AE=AB-AE
⇒PA=EB (equals subtracted from equals, the remainders are equals)
Therefore, ΔDBE≅ΔQAP (by RHS criteria)
conditions for congruence:
- ∠DBE=∠QAP=90°(right angle)
- PQ=ED(hypotenuse)
- PA=EB(side)
So, ∡D=∡Q(as congruent parts of congruent triangles are equal)