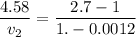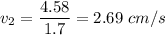Question

An aluminum sphere (specific gravity = 2.70) falling through water reaches a terminal speed of 4.58 cm/s. What is the terminal speed of an air bubble of the same radius rising through water? Assume viscous drag in both cases and ignore the possibility of changes in size or shape of the air bubble; Density of air at 20°c is 1.20 kg/m3 and that of water is 998.21 kg/m3.

Answer 1

Answer:2.69 cm/s

Step-by-step explanation:

We know that drag force

Fd=6 πμ r v

μ=Dynamic viscosity

r=radius

v=terminal velocity

Bouncy force

Fb= ρ V g

`rho_w=density\ of\ water`

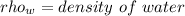
V=volume

At the condition of terminal velocity

when going down ( aluminum)

`Fb+ Fd= m g`

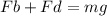
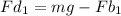`Fd_1 = m g - Fb_1`---------1

when going up ( air)

`Fb_2= mg +Fd`

`Fd_2= Fb_2 - mg`-----------2

m =mass of object

`m= density* volume`

`\rho_a=density\ of\ Aluminium`

`\rho _b=density\ of\ bubble`

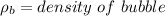
Divide 1 and 2

`(v_1)/(v_2)=(mg-F_b_1)/(F_b_2-mg)`

`(4.58)/(v_2)=(\rho _a-\rho _w)/(\rho _w-\rho _b)`

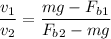
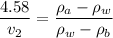
divide by
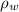`\rho _w` in R.H.S

`(4.58)/(v_2)=(2.7-1)/(1.-0.0012)`

`v_2=(4.58)/(1.7)=2.69\ cm/s`