Question

In a department of biology, there are five professors and five students. If seven members of the department are randomly selected to form a committee for admission, and if the number of professors must be one more than students, how many combinations are possible?

Answer 1

Answer: There are 50 ways to select in this way and there is only 1 combination is possible i.e. 3 students and 4 professors.

Explanation:

Since we have given that

Number of professors = 5

Number of students = 5

We need to find the number of ways of 7 members in such that number of professors must be one more than students.

So, if we select 3 students, then there will be 4 professors.

So, Number of ways would be

`^5C_3* ^5C_4\\\\=10* 5\\\\=50`

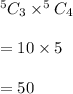
Hence, there are 50 ways to select in this way and there is only 1 combination is possible i.e. 3 students and 4 professors.