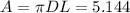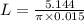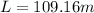Question

A counterflow double-pipe heat exchanger is used to heat water from 20°C to 80°C at a rate of 1.2 kg/s. The heating is to be completed by geothermal water available at 160°C at a mass flow rate of 2 kg/s. The inner tube is thin-walled and has a diameter of 1.5 cm. If the overall heat transfer coefficient of the heat exchanger is 640 W/m2K, determine the length of the heat exchanger required to achieve the required heating.

Answer 1

Answer:L=109.16 m

Step-by-step explanation:

Given

initial temperature
`=20^(\circ)C`

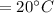
Final Temperature
`=80^(\circ)C`

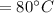
mass flow rate of cold fluid
`\dot{m_c}=1.2 kg/s`

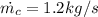
Initial Geothermal water temperature
`T_h_i=160^(\circ)C`

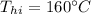
Let final Temperature be T

mass flow rate of geothermal water
`\dot{m_h}=2 kg/s`

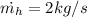
diameter of inner wall
`d_i=1.5 cm`

`U_(overall)=640 W/m^2K`

specific heat of water
`c=4.18 kJ/kg-K`

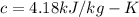
balancing energy

Heat lost by hot fluid=heat gained by cold Fluid

`\dot{m_c}c(T_h_i-T_h_e)= \dot{m_h}c(80-20)`

`2* (160-T)=1.2* (80-20)`

`160-T=36`

`T=124^(\circ)C`

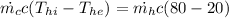
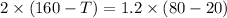
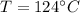
As heat exchanger is counter flow therefore

`\Delta T_1=160-80=80^(\circ)C`

`\Delta T_2=124-20=104^(\circ)C`

`LMTD=(\Delta T_1-\Delta T_2)/(\ln ((\Delta T_1)/(\Delta T_2)))`

`LMTD=(80-104)/(\ln (80)/(104))`

`LMTD=91.49^(\circ)C`

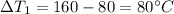
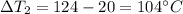
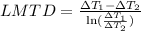
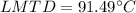
heat lost or gain by Fluid is equal to heat transfer in the heat exchanger

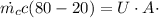`\dot{m_c}c(80-20)=U\cdot A\cdot` (LMTD)

`A=(1.2* 4.184* 1000* 60)/(640* 91.49)=5.144 m^2`

`A=\pi DL=5.144`

`L=(5.144)/(\pi * 0.015)`

`L=109.16 m`