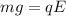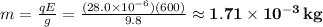Answer:
The mass of this object is
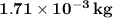
Step-by-step explanation:
If an object floats, it means by Newton’s second law that the sum of the forces acting on it are equal to zero because it’s at rest, as you can see on the figure below, the only two forces acting on the charged particle are the weight (W) and the electric force (Fe) due the electric field (E), so Newton’s second law in this case is:
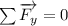
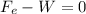
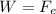 (1)
(1)
But weight is mass (m) times gravity acceleration (g) and the magnitude of the electric force is the product of the external electric field (E) and the charge of the particle (q), so using that on (1) and solving for m: