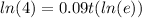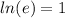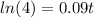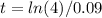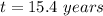Question

The population of a county is growing at a rate of 9% per year, compounded continuously. How many years will it take for the population to quadruple according to the exponential growth function?

Answer 1

`t=15.4\ years`

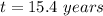
Explanation:

The exponential growth function compounded continuously is equal to

`A=P(e)^(rt)`

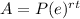
where

A is the final population

P is the initial population

r is the rate of growth in decimal

t is Number of years

e is the mathematical constant number

we have

`A=4x\\P=x\\ r=9\%=9/100=0.09`

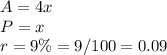
substitute in the function above

`4x=x(e)^(0.09t)`

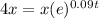
simplify

`4=(e)^(0.09t)`

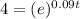
Take natural log of both sides

`ln(4)=ln[(e)^(0.09t)]`

`ln(4)=0.09t(ln(e))`

`ln(e)=1`

`ln(4)=0.09t`

`t=ln(4)/0.09`

`t=15.4\ years`